Neural Networking With Cocktails
By Jeff Lundy
While most people took up breadmaking during the pandemic, I got into cocktails. I don’t know how it took me so long to get into cocktails, as it basically combines chemistry with booze. As a nicety for my houseguests (whenever we have those again), I coded a menu website.

The website is powered by a Google spreadsheet that I maintain; and looking at the relationships between cocktail ingredients put me in the mind to brush up on network analysis. As a result, I ended up with some interesting insights into the cocktails Shannon and I like, and a method to suggest new cocktails based on the structural similarities between cocktails we already like.
THE BASIC NETWORK
Below you see the basic network among our most liked cocktails arranged using the Kamada/Kawai drawing algorithm. Essentially, this ‘force directed’ method treats each connection in the network as if it were a spring, and then ‘shakes’ the network so that nodes fly outward from their most connected neighbors. Loosely-connected nodes that are mainly connected to one ‘neighborhood’ will fly the furthest outward (e.g. Tequila), whereas tightly-connected nodes with connections to many regions of the graph will be pulled inward (e.g. Gin).
From the basic visual, you can see that Gin is the most central liquor in the network. This is mainly because Gin lies at the intersection of the cocktails that Shannon and I like. You can see that liquors like Tequila and Rum are less central. This is because they are less frequently on our favorite cocktail list, and because they tend to play with only certain sections of the network (e.g. most of the connections to Tequila are to juices).
Generally, you can see that liquors to the left of the “WhiteLiquor/Brown Liquor Line” (shown in red) are brown liquors, and ones to the right are white liquors (the one exception being Scotch; but that’s because I only have one Scotch cocktail on the list, and it’s a non-traditional one).
There are clearly some neighborhoods of similar ingredients. In the top left, there is a ‘French Quarter’ of ingredients often found in New Orleans drinks (e.g. Cognac, Absinthe, Benedictine, Peychaud’s bitters). Similarly, there is a juice neighborhood below gin that includes lemon, lime, and grapefruit juices, along with the juice-like ingredients of orange liqueur and orange bitters.
USING NETWORKS FOR PREDICTION
While basic visualization is one of the most powerful uses of network analysis, another important tool is the ability to predict new connections. Using a bit of network analysis, we should be able to predict new cocktail combinations that Shannon and I are likely to enjoy.
When I started this work, I thought I was going try out all kinds of cool ‘missing link’ predictors. These are varieties of the tools that Facebook and LinkedIn use to say: if Alice knows Bob, and Bob knows Carol, then maybe Alice knows Carol (or if she doesn’t, she might want to).
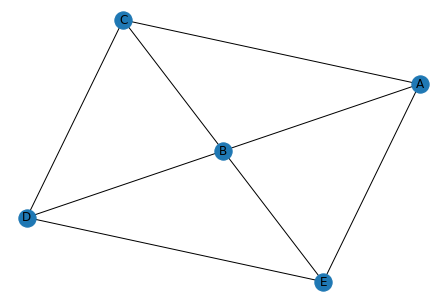
However, it didn’t take long for me to realize that there were already many novel cocktails just sitting in the network, without any missing link prediction! Consider the following example.
In the subgraph above, you can see that Gin is connected to Lemon Juice (both are in a Tom Collins, Bee’s Knees, Aviation, etc.), Lemon Juice is connected to Orgeat (through a Saturn and Hawaiian Sunset), Orgeat is connected to Aperol (both are in a Dead Man’s Handle), and Aperol is connected to Gin (through a High Five and a Negroni). In graph theory, when you can draw a complete polygon between a set of nodes, that’s called a cycle. This particular cycle may be of interest to us, because the proximity of the ingredients in the graph is not a coincidence – the Kamada/Kawai algorithm will tend to place ingredients close to each other based on shared relationships to the rest of the network. Also, we have a bit more connectivity here, as Orgeat is also connected to Gin (both are in a Saturn) and Lemon Juice is connected to Aperol (both are in a Part Time Lover). All signs suggest these ingredients play well together. However, there is not a cocktail on my list that includes all these ingredients at once.
In fact, when I searched Difford’s guide, and then Google, I only found one result for a cocktail using these ingredients (this blog post). This suggests that this ingredient combination might be novel to the broader cocktail world, not just to me and Shannon.
Reading the blog post, the author said he was trying to cross a Negroni with a Sour (clearly, he also wanted to play up the fruitiness of the drink, given his use of the Tiki ingredient Orgeat). The hybridization the author mentions is probably no accident. Interestingly, cocktail creation is not unlike the world of music composition.
ORIGINALITY AND AUTHENTICITY
When I was getting my undergrad degree in music composition, I wrote a piece that played off the similarity between a typical blues riff and the pentatonic scale employed in Russian folk music (Stravinsky uses it liberally in The Rite of Spring). It sounds like an odd fit, but because the two shared a similar 5-note structure, you got a piece that sounded both familiar and new at the same time.
The challenge of creating new combinations that are both pleasant and novel is something Richard Peterson wrote about in his great book Creating Country Music. Peterson mentioned that the A&M men who invented country music in the early 20th century had a saying: “Originality, Originality, and Authenticity.” This phrase expressed the seemingly contradictory challenge of their work. On the one hand, they needed original songs – people want to hear new things, and you can only copyright original pieces of music. However, they also needed songs that sounded like they were authentically old-timey – because that’s what was selling.
We face a similar situation as those A&M men: we want to identify combinations of ingredients that share a lot of similarity to past cocktails (so that they likely taste good together), but if we look for too much similarity to past cocktails, we won’t have any originality (we’ll make obvious swaps like switching out bourbon for rye in a Manhattan, or swapping vodka for gin in a Martini).
Fortunately, the search for new suggestions is helped by two factors: 1) the cocktail network is quite connected (there are lots of ways of finding new combinations among close connections), and 2) cocktails are usually only made of four or five ingredients. With just four or five nodes to connect, there are only a limited number of ways they can be connected in our graph, and we don’t need any fancy algorithms to identify strong interconnections.
When I ran the necessary code to identify combinations of four or five ingredients that are strongly connected in the network, I got back 8,508 results. Obviously, many of these subgraphs represent existing recipes or will share a great degree of similarity with them. Hence, to only find matches that exhibit enough originality, I removed all subgraphs sharing 3 or more ingredients with an existing recipe. The result is that we now have four- and five-ingredient cocktail recipes, that only overlap a pre-existing cocktail by at most two ingredients, but which have a strong chance of being tasty, given their network proximity to known good cocktails.
//////////TECHNICAL DEEP DIVE (SKIP IF YOU DON’T CARE HOW THIS WORKS)/////////
To find ingredients of interest in our original network graph, we are looking for signs of strong interconnection among 4- and 5-node groups.
So first, we want all 4- and 5-node cycles and cliques (i.e. where every node is connected to every other node).

Also, for our 4-node subgraphs we want those with at least 5 connections (called edges or vertices in graph theory). There can only be 6 total edges between 4 nodes, so ones with at least 5 edges have a high degree of interconnectivity.


For our 5-node subgraphs, the most limited form of interconnectivity we want is called a bowtie graph. The bowtie graph has only 6 edges for the five nodes, out of a total of 10 possible. Despite having a lower degree of connectivity, its structural relationship still suggests we might find a good hybrid, due to it combining two triangles. We also want any 5-node subgraphs with 7 or more edges (as those are just better-connected variants of the bowtie).

A quick note to data scientists on the usefulness of Python sets (or more technically, frozensets). An issue you face with many network projects is that practices to create linkages between nodes will generally create two sets of connections for each edge. For instance, I discovered a great hack to create the linkages between all nodes in the dataset: just use Pandas merge between a dataframe and itself – e.g. pd.Merge(cocktailIngredients, cocktailIngredients, on="COCKTAIL"). However, this naturally results in two rows for each ingredient combination, e.g.: Gin -> Aperol and Aperol -> Gin; which means that the same undirected link between Gin and Aperol is being expressed twice. Rather than do anything complicated to sort these out, I discovered the usefulness of Pandas’ sets.
If you make a new column filled with the frozenset of the combinations in each row, then the Gin -> Aperol and Aperol -> Gin rows will both now contain the same frozenset: {Gin, Aperol}. You must use a frozenset instead of a set, because Pandas can only iterate over sets that are stored as a frozenset. Then, applying the drop_duplicates function to this column you will be left with just one of the rows, no matter how they were ordered originally, because they now contain the same value. Similarly, my original function to identify all cycles included the starting node twice, e.g. Gin->Aperol->Lemon Juice->Orgeat->Gin. Converting to a set automatically fixed the issue, because the second Gin was automatically dropped once the first Gin was already a member.
HOW TO FIND THE BEST OF THE BEST?
Even after filtering, there were 166 strong candidates for potentially tasty cocktails. How to sort those according to the greatest likelihood for tastiness? Well, what’s good for the goose is good for the gander.
Originally, I created a graph to understand the underlying structure of the cocktails we like, and to see which ingredients are more isolated to the extremities. We can use the same trick again by drawing a graph among our strong candidate cocktails to see which ingredients are most novel (i.e. at the extremity of the graph).
I have to admit, I was surprised that this graph still exhibits a high degree of connectivity. Most nodes are connected to many other nodes, and there aren’t distinct neighborhoods or articulation points where one or two nodes link disparate parts of the graph. At this point, the visualization is only so helpful, and we need to turn to a couple of quantitative measures to help us.
Essentially, there are two ways we might find particularly strong candidates among our candidate list. One way is to look for combinations that likely taste good. To do this we can look at how ‘close’ the ingredients were in our original Kamada/Kawai graph. Ingredients that were closer in average distance will likely play better together. The other way we can hunt for the best candidates is to find those that are the most original. To do this, we sort for combinations that are closer to the extremity in our new graph of strong candidates.
//////////TECHNICAL DEEP DIVE (SKIP IF YOU DON’T CARE HOW THIS WORKS)/////////
Finding the ‘closeness’ of ingredients in our Kamada/Kawai graph is fairly easy to implement, as the closeness of the dots is just the area of the polygon they form. You can use the shoelace formula to find that area, once you get the x and y coordinates of each point from Networkx. Then you can divide their area by the number of nodes in the subgraph, to account for the fact that 5-node combinations will inherently be larger than 4-node combinations.
To quantify combinations that are closer to the extremity of the graph, we need to find the ‘group betweenness centrality’ (GBC) for the nodes in each combination. In short, if you find the shortest path between each node in the network, you can then count what proportion of these shortest paths go through any node. A node has a lot of betweenness if many of the shortest paths run through it. If you add together the betweenness centrality for each node among our strong candidates, you get their GBC. Again, getting this number is fairly easy as Networkx includes a group_betweenness_centrality function.
Once you have the GBC for each strong candidate, you can divide them by the number of nodes in the subgraph, to account for the fact that the sum of betweenness in 5-node combinations will inherently be greater than 4-node combinations. Then, we can sort by those with the lowest score. These are the cocktails at the extremities, because they represent cocktails with lower betweenness to the rest of the good candidate network.
THE WINNERS
Let me now introduce you to some delicious new cocktails…
The Graph Theory #1
This cocktail riffs on a Last Word but swaps the Maraschino and Lime Juice for Aperol and Lemon Juice. The result is a version that adds a beautiful orange flavor and color – proof that the network proximity of Gin, Lemon Juice, and Aperol in the network really does make for a tasty combination.

| Gin | 1 | oz |
| Aperol | 0.66 | oz |
| Green Chartreuse | 0.66 | oz |
| Lemon Juice | 0.66 | oz |
The Cycle
This cocktail is a hybrid of an Elderflower Margarita with a Tequila sunset. Floral flavors make this a less aggressive version of the Margarita.
| Tequila | 1.5 | oz |
| Elderflower Liqueur | 0.5 | oz |
| Orgeat | 0.25 | oz |
| Grenadine | 0.25 | oz |
| Lime Juice | 0.75 | oz |

The Clique
Not too revolutionary, but this cocktail swaps the gin in a French 75 for vodka, and then mixes it with a Grapefruit Mimosa.

| Vodka | 2 | oz |
| Grapefruit Juice | 2 | oz |
| Aperol | 0.5 | oz |
| Champagne | 1 | oz |
The Bowtie
A creative combination of an Elderflower Margarita and a Bella Luna (an Aviation riff with Elderflower liqueur). I would never have thought to put these together, but the overlap of Lime Juice and Elderflower liqueur means that this is a match made in heaven.
| Tequila | 2 | oz |
| Elderflower Liqueur | 0.5 | oz |
| Creme de Violette | 0.5 | oz |
| Maraschino | 0.25 | oz |
| Lime Juice | 0.75 | oz |

Other Posts by this Author
Image Sources
Dark cocktail
Mint cocktail
NN background
Red cocktail